anciendaze
Senior Member
- Messages
- 1,841
I've written elsewhere that distributions resulting from problems involving multiple interacting organ systems are very likely to be Lévy distributions, since efficiency of each system combines multiplicatively. A simple, obvious example is the combination of COPD and heart failure, and individuals with both problems function way below the mean, if they are still living.
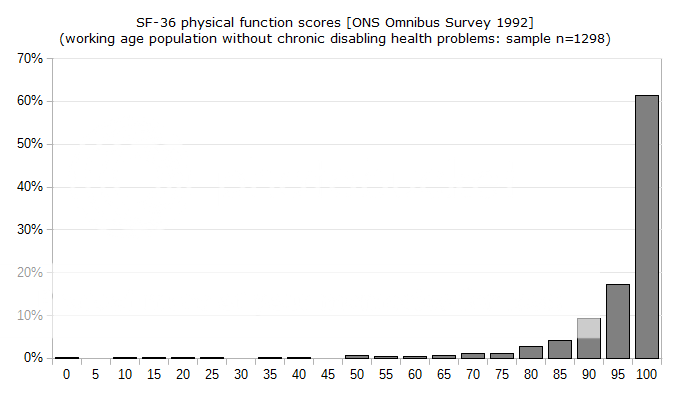
We don't really know if even the PACE authors believe the full distribution of SF-36 pf scores has a symmetrical right tail of people performing far above the mean. In the absence of such a tail the mean, mode and median values will not be the same, and common inferences about the meaning of "one-standard deviation below the mean" will be invalid. I suspect anyone familiar with psychology would know how readers who don't have the time to check all references and assumptions would interpret that criterion. Stated differently, I believe this continuing unresolved problem reflects a deliberate attempt to mislead.
From an academic standpoint, the distribution from which samples are drawn need not be Gaussian provided the Central Limit Theorem (CLT) applies. This places a great deal of weight on the sampling process itself, plus some unstated assumptions. What we know in this case is that patients entering the trial were chosen according to subjective values applied by a small group of people. It is hard to find objective criteria for the illness definition in use. A small sprinkling of randomness will not correct inherent systematic bias.
I think the common prerequisites for the CLT, independent identically-distributed random processes, are clearly not present. More sophisticated proofs of the CLT depend on a large number of different distributions, each possessing a mean and bounded variance. Analytic Lévy distributions do not have bounded variance. It seems quite likely they have mixed samples with organic disease and psychological problems. I do not consider two a large number. If the organic disease(s) involved combine multiplicatively to reduce performance, the main requirement for getting a Gaussian distribution out disappears entirely.
We don't know how many times they applied sampling criteria before they got something out that looked like a set of normal distributions for each group. We do know they had so much trouble getting the numbers they wanted that they went back and revised the entry criteria. If changing these by 5 points did not invalidate results, then, a fortiori, changing a score by 5 points during the trial will not invalidate the null hypothesis that there was no benefit. This implies that modified recovery criteria should be more stringent, not less.
Do we have any way to evaluate the number of patients considered recovered by no more than 5 points?
In the absence of answers to the objections above, I believe we should consider the entire 5-million pound study an expression of unsubstantiated opinion.
We don't really know if even the PACE authors believe the full distribution of SF-36 pf scores has a symmetrical right tail of people performing far above the mean. In the absence of such a tail the mean, mode and median values will not be the same, and common inferences about the meaning of "one-standard deviation below the mean" will be invalid. I suspect anyone familiar with psychology would know how readers who don't have the time to check all references and assumptions would interpret that criterion. Stated differently, I believe this continuing unresolved problem reflects a deliberate attempt to mislead.
From an academic standpoint, the distribution from which samples are drawn need not be Gaussian provided the Central Limit Theorem (CLT) applies. This places a great deal of weight on the sampling process itself, plus some unstated assumptions. What we know in this case is that patients entering the trial were chosen according to subjective values applied by a small group of people. It is hard to find objective criteria for the illness definition in use. A small sprinkling of randomness will not correct inherent systematic bias.
I think the common prerequisites for the CLT, independent identically-distributed random processes, are clearly not present. More sophisticated proofs of the CLT depend on a large number of different distributions, each possessing a mean and bounded variance. Analytic Lévy distributions do not have bounded variance. It seems quite likely they have mixed samples with organic disease and psychological problems. I do not consider two a large number. If the organic disease(s) involved combine multiplicatively to reduce performance, the main requirement for getting a Gaussian distribution out disappears entirely.
We don't know how many times they applied sampling criteria before they got something out that looked like a set of normal distributions for each group. We do know they had so much trouble getting the numbers they wanted that they went back and revised the entry criteria. If changing these by 5 points did not invalidate results, then, a fortiori, changing a score by 5 points during the trial will not invalidate the null hypothesis that there was no benefit. This implies that modified recovery criteria should be more stringent, not less.
Do we have any way to evaluate the number of patients considered recovered by no more than 5 points?
In the absence of answers to the objections above, I believe we should consider the entire 5-million pound study an expression of unsubstantiated opinion.